Máximos y mínimos

MÁXIMOS Y MÍNIMOS

Los puntos críticos permiten determinar los valores máximos o valores mínimos que alcanza la función. El punto crítico que se encuentra en el intervalo de una concavidad que abre hacia abajo permite determinar el valor máximo que alcanza la función y el que se encuentra en una concavidad que abre hacia arriba, al mínimo que alcanza la función.

Criterio de la primera derivada:

•Se determinan los intervalos de crecimiento y decrecimiento.

•Existe máximo relativo en los puntos en que la función pasa de creciente a decreciente.

•Existe mínimo relativo en los puntos en que pasa de decreciente a creciente.

 

Criterio de la segunda derivada:

•Calculamos la primera derivada, la igualamos a cero y resolvemos la ecuación resultante.

•Hallamos la segunda derivada.

•Las raíces de la ecuación obtenida se sustituyen en la segunda derivada.

•Si el resultado obtenido es positivo existe mínimo y si es negativo máximo.

Crecimiento y decrecimiento.

Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:

*Una función f(x) es creciente en un punto a, si su derivada es positiva

*Una función f(x) es decreciente en un punto a, si su derivada es negativa.

                                    Se procede de la siguiente forma:

 • Se halla la derivada, se iguala a cero y se resuelve la ecuación resultante.

 

• Con los puntos en los que se anula la derivada dividimos el dominio en intervalos.

• Se estudia el signo de la derivada en un punto cualquiera de cada uno de los intervalos resultantes.

-Punto máximo -> creciente-decreciente: En ese valor de x donde f'(x)=0, hay un máximo.

Punto mínimo -> decreciente-creciente: En ese valor de x donde f'(X)=0, hay un mínimo.

Los máximos y mínimos son puntos que necesitan las dos coordenadas (x , y)

Para calcular la coordenada "y" de los máximos y mínimos, sustituimos el valor de x en la función.

Ejemplo:

f(x)= 1/4x^4 - 2x^2
-Obtenemos primera derivada:

f'(x)= x^3-4x
-Igualamos f'(x)= 0 para obtener puntos criticos
x^3 -4x= 0
x(x^2-4)= 0
x= 0 y x = +2/-2

-Nuestros puntos criticos serán 0,-2,+2
-Ahora obtenemos la segunda derivada
f''(x)= 3x^2-4
-Evaluamos los puntos criticos en la segunda derivada
f''(0)= -4 -> por lo tanto hay un máximo en x= 0

f''(-2)= 8 ->por lo tanto hay un mínimo en x= -2
f''(+2)= 8 -> por lo tanto hay un minimo en x= +2                                                      

-Los puntos de inflexion se obtienen igualando a cero la segunda derivada f''(x)= 0
3x^2-4=0
-Nuestros puntos de inflexión serán +raiz4/3 y -raiz4/3
concava hacia arriba (-ºº, -raiz4/3)U(+raiz4/3, +ºº)
concava hacia abajo (-raiz4/3, +raiz4/3)



Ejemplo 1

Consideremos la siguiente función:
Entonces:
Esta función es constante, para cualquier punto de su dominio vale 5 (por eso f(x+h)=5). Nótese el último paso, donde h tiende a cero pero nunca lo alcanza. Si pensamos un poco, observaremos que la derivada además de ser la pendiente de la recta tangente a la curva, es a la vez, la recta secante a la misma curva.

Ejemplo 2

Consideremos la gráfica de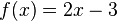 . Esta recta tiene una pendiente igual a 2.0 en cada punto. Utilizando el cociente mostrado arriba (junto a los conceptos de limite, secante, y tangente) podremos determinar las pendientes en los puntos 4 y 5:
Entonces:
Y vemos que se cumple para cualquier número n:
Por tanto, se deduce que el valor de la función derivada de una recta es igual a la pendiente de la misma.

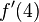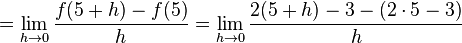Ejemplo 3

Mediante esta diferenciación, se puede calcular la pendiente de una curva. Consideremos que: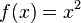
Entonces: