Funciones Exponenciales y Logaritmicas

LA FUNCIÓN EXPONENCIAL
Definición. Sea  a  un número real positivo. La función que a cada número real x le hace corresponder la potencia  a˟ se llama función exponencial de base a y exponente x.                                                Como para  a˟˃0  todo x€Ɍ  ,la función exponencial es una función de Ɍ en Ɍ. En el siguiente teorema, se presentan las propiedades más importantes de la función exponencial.                                                                       Teorema (Leyes de los Exponentes) Sean a y b reales positivos y x,yÎÂ ,entonces: Cuando a > 1 ,si x < y, entonces, .Es decir, cuando la base a es mayor que 1,la función exponencial de base a es estrictamente creciente en su dominio. Cuando 0 < a < 1, si x < y , entonces, . Esto significa que la función exponencial de base a < 1 es estrictamente decreciente en su dominio. . 10.Si 0< a < b ,se tiene: . Esta propiedad permite comparar funciones exponenciales de diferentes bases. 11. Cualquiera que sea el número real positivo  ,existe un único número real   tal que . Esta propiedad indica que la función exponencial es sobreyectiva. Cuando x e y son enteros, los propiedades enunciadas anteriormente pueden demostrarse usando las definiciones y el teorema 1. Para el caso en el cual x e y son racionales, la demostración utiliza la definición y el teorema 2. Para el caso general, es decir, cuando x e y son reales, la demostración utiliza elementos del análisis real.                                                            Gráfica de la Función Exponencial
 Note que cuando la base a es mayor que 1,la función exponencial (fig.1) no está acotada superiormente. Es decir , crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es , tiende a cero(0), cuando x toma valores grandes pero negativos.                                                                                 Igualmente, cuando la base a < 1, la función exponencial fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así, crece sin límite, al tomar x valores grandes, pero negativos y tiende a cero, cuando la variable x toma valores grandes positivos.                                                    El hecho de ser la función exponencial  con a > 1, estrictamente creciente (estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se presentan en la próxima sección. En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición de función; y, en otro, del hecho de ser la función exponencial inyectiva. Observación. Cuando a = e ,donde e es el número irracional cuya representación decimal con sus primeras cifras decimales, es e = 2.7182818284….,la función exponencial ,se llama: función exponencial de base e y, frecuentemente, se denota por Exp( x ) =                                    Potencias, logaritmos y su relación El producto de n factores iguales a a: n a · a · ... · a, se llama potencia de base a y exponente n, donde a ð 0 ó n ð 0. Es de suponer que no sea una operación conmutativa, ya que base y exponente cumplen funciones distintas. (La demostración queda conforme con sólo ver que 23 ð 32). Algunas propiedades son: a0 = 1; 00 no tiene sentido. El producto de potencias de igual base es una potencia de la misma base que tiene por exponente la suma de los exponentes. n m n+m an · am = a · a · ...· a · a · a · ...· a = a · a · ...· a = an+m El producto de potencias de igual e ponente es igual a una potencia del mismo exponente que tiene por base el producto de las bases.

Funciones Trigonometricas

Funciones Trigonometricas

DIRECTAS:

La trigonometría en principio es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos. En términos generales, la trigonometría es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante.

1) El seno del ángulo es la relación entre el cateto opuesto y la hipotenusa.

2) El coseno del ángulo es la relación entre el cateto adyacente y la hipotenusa.

3) La tangente del ángulo es la relación entre el cateto opuesto y el cateto adyacente.

4) La cosecante del ángulo es la relación entre la hipotenusa y el cateto opuesto.

5) La secante del ángulo es la relación entre la hipotenusa y el cateto adyacente.

6) La cotangente del ángulo es la relación entre el cateto adyacente y el opuesto.

 

 

Gráficas de las Funciones Trigonométricas Directas

SENO HIPERBÓLICO: Gráfica de y = sen

 

COSENO HIPERBÓLICO: Gráfica de y = cos x 

TANGENTE HIPERBÓLICA: Gráfica de y = tg x

COTANGENTE HIPERBÓLICA:Grafica de y=ctg x

 SECANTE HIPERBÓLICA:Grafica de y=sec x

 

                                          

 COSECANTE HIPERBÓLICA:Grafica de y=cnt x

INVERSAS:   GRAFICAS DE LAS FUNCIONES HIPERBÓLICAS 

La funciones inversas de las funciones trigonométricas son: arco seno, arco coseno, arco tangente, arco cosecante, arco secante y arco cotangente.

Las tres funciones trigonométricas inversas usadas de manera común son:

1) Arcoseno: es la función inversa del seno del ángulo.

2) Arcocoseno: es la función inversa del coseno del ángulo.

3) Arcotangente: es la funcion inversa de la tangente del ángulo.

Derivada potencial-exponencial

Arcoseno HIPERBÓLICO INVERSO              

arcocoseno HIPERBÓLICO INVERSO

  arcotangente HIPERBÓLICA INVERSA

 

arcosecante HIPERBÓLICA INVERSA

arcocosecante HIPERBÓLICA INVERSA

 

arcotangente HIPERBÓLICA INVERSA

Derivadas Sucesivas

Derivadas Sucesivas

Si derivamos la derivada de una función, derivada primera, obtenemos una nueva función que se llama derivada segunda, f''(x).

Si volvemos a derivar obtenemos la derivada tercera, f'''(x).

Si derivamos otra vez obtenemos la cuarta derivada f'^v y así sucesivamente.

Calcula las derivadas 1ª, 2ª, 3ª y 4ª de:

Derivada enésima

En algunos casos, podemos encontrar una fórmula general para cualquiera de las derivadas sucesivas (y para todas ellas). Esta fórmula recibe el nombre de derivada enésima, f'ⁿ(x).

Criterio del signo de la derivada primera

En lo sucesivo vamos a tratar con funciones continuas y derivables. En un curso superior sobre derivadas se considerarán otras situaciones. 

Ya vimos que hay una relación entre la monotonía de la función f(x) (crecimiento ó decrecimiento) y el valor de la derivada primera f ´(x).

f(x) creciente: f ´(x) > 0

f(x) decreciente: f ´(x) < 0

También veíamos que en los puntos donde la función cambia de creciente a decreciente o de decreciente a creciente la derivada se hace cero f ´(x) = 0 ya que el cambio de signo de la derivada se hace con continuidad y necesariamente tiene que pasar por el valor 0.

 

Criterio del signo de la derivada segunda

En un punto x = a donde la exista un máximo local la derivada primera cambia de signo de f ´ > 0 a f ´ < 0, esto significa que la derivada primera f ´(x) pasa decreciendo por el punto x=a, necesariamente la derivada segunda tiene que ser negativa

f ´´(a) < 0

En un punto x = a donde exista un mínimo local la derivada primera cambia el signo de f ´< 0 a f ´ > 0, esto significa que la derivada primera f ´(x) pasa creciendo por el punto x = a, necesariamente la derivada segunda tiene que ser positiva

f ´´(a) > 0

                                                                                

Donde	habrá	siempre que
f ´(a) = 0	Máximo local	f ´´(a) < 0
	Mínimo local	f ´´(a) > 0

Veamos ahora cómo se puede resolver el problema de hallar máximos y mínimos con el criterio de la derivada segunda.

En el Ejemplo 1 nos daban la función f(x) = x³- 6x²+9x+2. 

Se calculan las derivadas sucesivas f ´(x) = 3x²-12x+9, f ´´(x) = 6x-12

Continuidad de una Funcion

Continuidad de una Funcion.

Definición

Continuidad

Una función f(x) es continua en un punto a si lim_x->af(x) = f(a).

Nota: observar que debe existir f(a) y debe existir el lim_x->a f(x) y debe ser igual a f(a). 

f(x)=x²

Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva. 

 

En contraste, una gráfica como la de la función f(x) = sgn x (signo de x) que consiste de pedazos de curva separados por un vacío en una abcisa exhibe allí una discontinuidad.

La continuidad de la función f(zx) para un valor a significa que f(x) difiere arbitrariamente poco del valor f(a) cuando x está suficientemente cerca de a.

Expresemos esto en términos del concepto de límite...

Teorema

Continuidad de la función compuesta

H) f es continua en x=a.
g es continua en x=f(a).
T) g o f es continua en x=a.

Demostración:

Queremos demostrar que lim_x->a g[f(x)]=g[f(a)], o sea, por definicion por limite, queremos probar que, dado ε>0 existe δ>0 tal que para todo x perteneciente al E^*_a,δ g[f(x)] perteneciente al E_g[f(a)],ε.

Por hipótesis g es continua en f(a) => por def. de continuidad lim_x->f(a) g(x)=g[f(a)] => por def. por limite dado ε>0 existe δ>0 tal que...

para todo x perteneciente al E^*_f(a),δ g(x) pertenece al E_g[f(a)],ε (1)

Por hipótesis f es continua en a => por def. de continuidad lim_x->af(x) = f(a), es decir que (por def. de limite) si tomamos el número δ de (1), existe α>0 tal que...

para todo x perteneciente al E^*_a,α f(x) pertenece al E_f(a),δ (2) 

 

De (1) y (2) se deduce que:
Dado ε>0 existe α>0 / para todo x perteneciente al E^*_a,α g[f(x)] pertenece al E_g[f(a)],ε. 

1.-Estudiar la continuidad de la función f(x) = x · sgn x.

2.-Estudiar la continuidad en x = 0 de la función:

3.-Calcular el valor de a para que la función siguiente sea continua:

4.-La función definida por:

es continua en [0, ∞).

5Dada la función:

1 Demostrar que f(x) no es continua en x = 5.

2¿Existe una función continua que coincida con f(x) para todos los valores x ≠ 5? En caso afirmativo dar su expresión.

Máximos y mínimos

MÁXIMOS Y MÍNIMOS

Los puntos críticos permiten determinar los valores máximos o valores mínimos que alcanza la función. El punto crítico que se encuentra en el intervalo de una concavidad que abre hacia abajo permite determinar el valor máximo que alcanza la función y el que se encuentra en una concavidad que abre hacia arriba, al mínimo que alcanza la función.

Criterio de la primera derivada:

•Se determinan los intervalos de crecimiento y decrecimiento.

•Existe máximo relativo en los puntos en que la función pasa de creciente a decreciente.

•Existe mínimo relativo en los puntos en que pasa de decreciente a creciente.

 

Criterio de la segunda derivada:

•Calculamos la primera derivada, la igualamos a cero y resolvemos la ecuación resultante.

•Hallamos la segunda derivada.

•Las raíces de la ecuación obtenida se sustituyen en la segunda derivada.

•Si el resultado obtenido es positivo existe mínimo y si es negativo máximo.

Crecimiento y decrecimiento.

Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:

*Una función f(x) es creciente en un punto a, si su derivada es positiva

*Una función f(x) es decreciente en un punto a, si su derivada es negativa.

                                    Se procede de la siguiente forma:

 • Se halla la derivada, se iguala a cero y se resuelve la ecuación resultante.

 

• Con los puntos en los que se anula la derivada dividimos el dominio en intervalos.

• Se estudia el signo de la derivada en un punto cualquiera de cada uno de los intervalos resultantes.

-Punto máximo -> creciente-decreciente: En ese valor de x donde f'(x)=0, hay un máximo.

Punto mínimo -> decreciente-creciente: En ese valor de x donde f'(X)=0, hay un mínimo.

Los máximos y mínimos son puntos que necesitan las dos coordenadas (x , y)

Para calcular la coordenada "y" de los máximos y mínimos, sustituimos el valor de x en la función.

Ejemplo:

f(x)= 1/4x^4 - 2x^2
-Obtenemos primera derivada:

f'(x)= x^3-4x
-Igualamos f'(x)= 0 para obtener puntos criticos
x^3 -4x= 0
x(x^2-4)= 0
x= 0 y x = +2/-2

-Nuestros puntos criticos serán 0,-2,+2
-Ahora obtenemos la segunda derivada
f''(x)= 3x^2-4
-Evaluamos los puntos criticos en la segunda derivada
f''(0)= -4 -> por lo tanto hay un máximo en x= 0

f''(-2)= 8 ->por lo tanto hay un mínimo en x= -2
f''(+2)= 8 -> por lo tanto hay un minimo en x= +2                                                      

-Los puntos de inflexion se obtienen igualando a cero la segunda derivada f''(x)= 0
3x^2-4=0
-Nuestros puntos de inflexión serán +raiz4/3 y -raiz4/3
concava hacia arriba (-ºº, -raiz4/3)U(+raiz4/3, +ºº)
concava hacia abajo (-raiz4/3, +raiz4/3)



Ejemplo 1

Consideremos la siguiente función:
Entonces:
Esta función es constante, para cualquier punto de su dominio vale 5 (por eso f(x+h)=5). Nótese el último paso, donde h tiende a cero pero nunca lo alcanza. Si pensamos un poco, observaremos que la derivada además de ser la pendiente de la recta tangente a la curva, es a la vez, la recta secante a la misma curva.

Ejemplo 2

Consideremos la gráfica de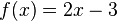 . Esta recta tiene una pendiente igual a 2.0 en cada punto. Utilizando el cociente mostrado arriba (junto a los conceptos de limite, secante, y tangente) podremos determinar las pendientes en los puntos 4 y 5:
Entonces:
Y vemos que se cumple para cualquier número n:
Por tanto, se deduce que el valor de la función derivada de una recta es igual a la pendiente de la misma.

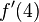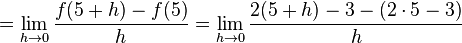Ejemplo 3

Mediante esta diferenciación, se puede calcular la pendiente de una curva. Consideremos que: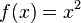
Entonces: